Significance refers to generalization to the population from sample statistics. When sample statistics are close to population statistics or the parameters, generalization becomes easy.
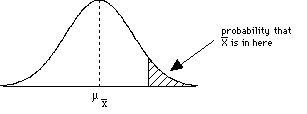
The central limit theorem tells us that, if our sample is large, the sampling distribution of the mean will be approximately normally distributed irrespective of the shape of the population distribution. Before use of statistical tools, it is important to estimate to what extent the data represent all the assumptions of specific tools. Below are some of the assumptions of repeatedly used bi-variate statistics for mean differences.
1. t-ratio
1.1. Testing for Normality
1.2 Homogeneity of variance (homoscedasticity) is an important assumption shared by many parametric statistical methods. This assumption requires that the variance within each population be equal for all populations (two or more, depending on the method). For example, this assumption is used in the two-sample t-test and ANOVA. If the variances are not homogeneous, they are said to be heterogeneous. If this is the case, we say that the underlying populations, or random variables, are heteroscedastic (sometimes spelled as heteroskedastic).(ref: http://link.springer.com/referenceworkentry/10.1007%2F978-3-642-04898-2_590)
2. F-ratio
t-test, Z-test and F-tests are used for assessing tests of significance in mean differences when distribution follows normality assumptions.
All parametric tests assume that the populations have specific characteristics and that samples are drawn under certain conditions. These characteristics and conditions are expressed in the assumptions of the tests.
Ref:http://www.psychology.emory.edu/clinical/bliwise/Tutorials/TOM/meanstests/assump.htm
One-Sample Z Test
The assumptions of the one-sample Z test focus on sampling, measurement, and distribution. The assumptions are listed below. One-sample Z tests are considered "robust" for violations of normal distribution. This means that the assumption can be violated without serious error being introduced into the test. The central limit theorem tells us that, if our sample is large, the sampling distribution of the mean will be approximately normally distributed irrespective of the shape of the population distribution. Knowing that the sampling distribution is normally distributed is what makes the one-sample Z test robust for violations of the assumption of normal distribution.
|
|
|
One-Sample t Test
The assumptions of the one-sample t-test are identical to those of the one-sample Z test. The assumptions are listed below. One-sample t-tests are considered "robust" for violations of normal distribution. This means that the assumption can be violated without serious error being introduced into the test.
|
|
|
t-Test for Dependent Means
The assumptions of the t-test for dependent means focus on sampling, research design, measurement, and distribution. The assumptions are listed below. The t-test for dependent means is considered typically "robust" for violations of normal distribution. This means that the assumption can be violated without serious error being introduced into the test in most circumstance. However, if we are conducting a one-tailed test and the data are highly skewed, this will cause a lot of error to be introduced into our calculation of difference scores which will bias the results of the test. In this circumstance, a nonparametric test should be used.
|
|
|
|
t-Test for Independent Means
The assumptions of the t-test for independent means focus on sampling, research design, measurement, population distributions and population variance. The assumptions are listed below. The t-test for independent means is considered typically "robust" for violations of normal distribution. This means that the assumption can be violated without serious error being introduced into the test in most circumstance. However, if we are conducting a one-tailed test and the data are highly skewed, this will cause a lot of error to be introduced into our test and a nonparametric test should be used. The t-test for independent means is not robust for violations of equal variance. Remember that the shape of the sampling distribution is determined by the population variance (s2) and the sample size. If the population variances are not equal, then when we calculate the difference between sample means, we do not have a sampling distribution with an expectable shape and cannot calculate an accurate critical value of the t distribution. This is a serious problem for our test. Our alternatives when the asssumption of equal variances has been violated are to use a correction (available in the SPSS program) or to use a nonparametric test. How do we determine whether this assumption has been violated? Conduct a Levene's test (using SPSS).
|
|
|
|
|
z-test is preferable when n is greater than 30.
the distributions should be normal if n is low, if however n>30 the distribution of the data does not have to be normal
the variances of the samples should be the same (F-test)
all individuals must be selected at random from the population
all individuals must have equal chance of being selected
sample sizes should be as equal as possible but some differences are allowed
where n<30 the t-tests should be used
the distributions should be normal for the equal and unequal variance t-test (K-S test or Shapiro-Wilke)
the variances of the samples should be the same (F-test) for the equal variance t-test
all individuals must be selected at random from the population
all individuals must have equal chance of being selected
sample sizes should be as equal as possible but some differences are allowed
Z-test and t-test are basically the same; they compare between two means to suggest whether both samples come from the same population. There are however variations on the theme for the t-test. If you have a sample and wish to compare it with a known mean (e.g. national average) the single sample t-test is available. If both of your samples are not independent of each other and have some factor in common, i.e. geographical location or before/after treatment, the paired sample t-test can be applied. There are also two variations on the two sample t-test, the first uses samples that do not have equal variances and the second uses samples whose variances are equal.
It is well publicised that female students are currently doing better then male students! It could be speculated that this is due to brain size differences? To assess differences between a set of male students' brains and female students' brains a z or t-test could be used. This is an important issue (as I'm sure you'll realise lads) and we should use substantial numbers of measurements. Several universities and colleges are visited and a set of male brain volumes and a set of female brain volumes are gathered (I leave it to your imagination how the brain sizes are obtained!).
Excel can apply the z or t-tests to data arranged in rows or in columns, but the statistical packages nearly always use columns and are required side by side.
Degrees of freedom:
For unequal and equal variance t-tests = (n1 + n2) - 2
For paired sample t-test = number of pairs - 1
The output from the z and t-tests are always similar and there are several values you need to look for:

You can check that the program has used the right data by making sure that the means (1.81 and 1.66 for the t-test), number of observations (32, 32) and degrees of freedom (62) are correct. The information you then need to use in order to reject or accept your HO, are the bottom five values. The t Stat value is the calculated value relating to your data. This must be compared with the two t Critical values depending on whether you have decided on a one or two-tail test (do not confuse these terms with the one or two-way ANOVA). If the calculated value exceeds the critical values the HO must be rejected at the level of confidence you selected before the test was executed. Both the one and two-tailed results confirm that the HO must be rejected and the HA accepted.
We can also use the P(T<=t) values to ascertain the precise probability rather than the one specified beforehand. For the results of the t-test above the probability of the differences occurring by chance for the one-tail test are 2.3x10-9 (from 2.3E-11 x 100). All the above P-values denote very high significant differences.
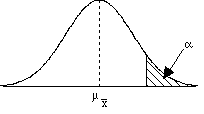
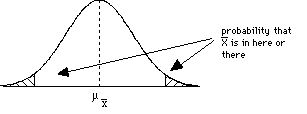
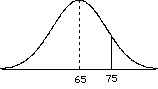
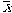 = 69.Did the treatment work? Does it affect the population of individuals?
= 69.Did the treatment work? Does it affect the population of individuals?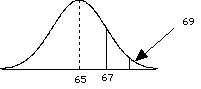
 =
=  = 10/5 = 2
= 10/5 = 2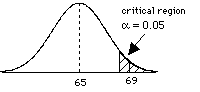
 = (69 - 65) / 2 = 2.0 since > Zcritical, then we can reject the H0
= (69 - 65) / 2 = 2.0 since > Zcritical, then we can reject the H0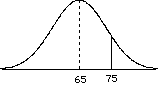
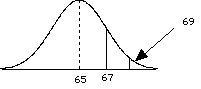
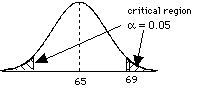
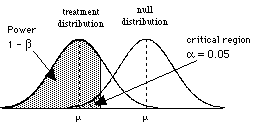
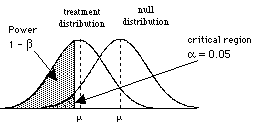
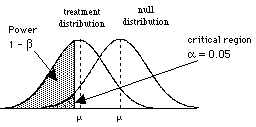
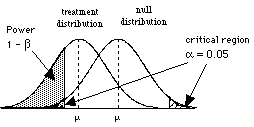
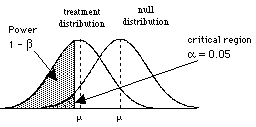
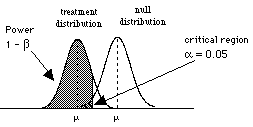
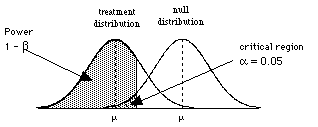 So to consider power, we need to consider the situation where H0 is wrong, that is when there are two populations, the treatment population and the null population
So to consider power, we need to consider the situation where H0 is wrong, that is when there are two populations, the treatment population and the null population